COLOCON 2018 予選
作成日:2017.12.10
カテゴリー:競プロ 参戦記録
目次
コンテスト前の計画
配点が$100-200-400-500-700$なので、早解きするしかない。
ただ誤答ペナルティがあるので、コードを書いたらとりあえず提出する作戦はとりづらい。
コンテスト中
A,B,C問題はすぐに解くことができた。[A 01:56 AC][B 04:32 AC][C 13:06 AC]
D問題は$O(N^3)$から落とすためにセグメントツリーを使うように見えたのでそうする。
細かいところで手間取ったがサンプルが合ったので提出したが通らない。[D 51:43 TLE]
TLEをもらったので、計算量のlogを落とそうと考える。
maxを取るタイミングを上手くすると良さそうだったのでそうする。
若干考察が怪しかったが、TLEをもらって焦っていたのでとりあえず提出。[D 67:48 MLE]
MLEはlong longで$5000 \times 5000$の配列を2個も取っていたのが原因なのはすぐに気づいた。
配列を使いまわすように変更して提出。[D 70:13 AC]
D問題でTLEとMLEをもらってパニック状態にある中、E問題を解き始める。
しばらくして、これを組み合わせれば良さそうという部品を思いつく。
その後部品をどのように組み合わせるかの考察がサンプルに引っ張られる形で若干手間取ったが、何とか構成しきった。
それをコードに落として提出。[E 107:28 WA]
通ると思い込んでいたので完全にパニックになったので、デバッグできないまま時間切れ。
コンテスト後(結果)
4完1200点の45位。レート変動なし。
D問題でちゃんと考察すれば$O(N^2)$になるのに、すぐに見えたセグメントツリーを用いる解法に飛びついたのは反省。
E問題は焦りながら解いていたのがバグにつながったと思われる。
焦っても良いことはないのだが早解きだと思うと焦ってしまうので、その点は今後どう解消するかが課題である。
各問題の(軽い)解説
A : すぬけそだて――登録――
問題文
文字列をstringで持てば、size関数を用いて楽に判定できる。
B : すぬけそだて――チュートリアル――
問題文
「ローディング」の時は、そのままの時間がかかる。
しかし「ストーリー」の時は、そのままの時間と$X$のいずれかを選ぶことができる。
時間を最小にしたいのだから、選べる時は小さい方を選べば良い。
C : すぬけそだて――ごはん――
問題文
選べる整数の差は$35$を超えないから、$35$より大きい数で割り切れるのは1つしかない。
よって$35$以下の数で割り切れる整数を選んだかを保持しながらカードを選んでいけば良いが、このままだと状態が多すぎる。
互いに素になるようにするためには素数についてのみ保持していても問題はなく、こうすることで状態数が十分少なくなる。
D : すぬけそだて――トレーニング――
問題文
すぐに思いつくのは$i$番目の候補まで見て$j$個の候補をすでに選んだこと(以下$(i,j)$とする)を状態に持つDPであるが、愚直に求めると計算量が$O(N^3)$であり間に合わない。
$(i,j+1)$は$max[(z,j)$$+d]$$(z < i)$である。
$d$は$T_z + X < T_i$の時$X$、そうでない時$T_i - T_z$である。
このままだとSegment Treeを使い$O(N^2 log \: N)$になるが、これは間に合うか微妙である。
そこで貰うDPではなく配るDPにすることを考える。
$(i,j)$が配る先は$(y,j+1)$$(y>i)$であり、答えの増加量は$T_i + X < T_y$の時$X$、そうでない時$T_y - T_i$である。
前者と後者の境界となる$y$を$b$とし、$y > b$の時に前者の場合になるとする。
前者は配る時に$i = b + 1$に値を持っておくようにすれば、配り終えた後に$i$の小さい方から$max$を取っていくことで求めることができる。
後者も同じように$i = b$に値を持って、$i$の大きい方から$max$を取っていくことで処理したい。
持っておくべき値は、各項で共通である元の値から$T_i$を引いたものである。
$max$を取った後に$T$を足せば、その位置での値を求めることができる。
後は元々$max$を取るべきでない位置にも影響してしまうことが問題なければ良い。
これは範囲外では$j = a$の時の値を越えないということと、$j$が大きくなれば答えは小さくならないということから分かる。
前者と後者のうち大きい方がその状態での答えとなる。
以上の方法の計算量は$O(N^2)$であるから十分高速である。
E : すぬけそだて――わっか――
問題文
$5000$個の点を選んで平面を最大$10^6$個に分割しなければならないので、選んだ点の数の二乗程度に分割で切る方法を見つけなければならない。
これには様々な方法があるが、以下では私がコンテスト中に思いついたものを紹介する。
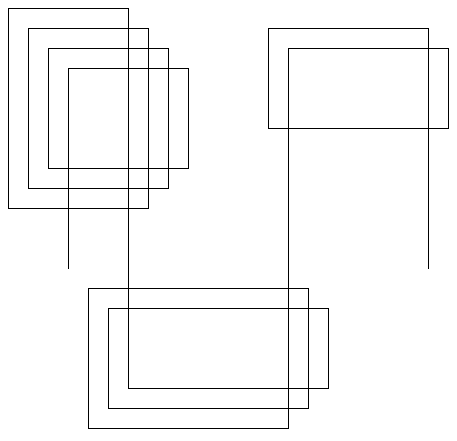
以下の図において、渦巻き状になっている部品で$n$回巻きのものは線分で閉じた部分を$n^2$個生成する。
これは約$4n$個の点を用いることで作ることができる。
$\sum{n_i^2}$$=K-1$が成り立つように$i$個目の部品の巻き数$n_i$を決めていき、図のように部品を連結させれば構成できる。
<(古い記事)
関連
<(古い記事) CODE FESTIVAL 2017 Team Relay
Topcoder Marathon Match 96 (新しい記事)>